proyecciones ortogonales

COLEGIO NACIONAL AMAZONAS

TRABAJO INTEGRADOR DE INFORMÁTICA

Licda: Verónica Zandumbide

Nombre: Daniel Reascos

Curso: 1ro de bachillerato sexta Sección

TEMA:Proyecciones ortogonales

Asignatura:Dibujo Tecnico

Proyección ortogonal

Objetivo General

La Geometría Descriptiva, o Método Monge, es un método para producir “la representación plana de un objeto de modo que pueda definirse con precisión la distribución y dimensiones de sus elementos constitutivos”.

Objetivos Especificos 

Hay dos características que lo diferencian de otros métodos de dibujo: la precisión y el desdoblamiento de las visiones del objeto. 

La perspectiva presenta ambigüedades, ya que no puede definirse la ubicación exacta de los puntos representados. Por ejemplo en la perspectiva de la figura 1 hay una línea que puede 

ser tanto la diagonal de la cara lateral como la prolongación de la línea ab.

Marco teorico

En geometría euclidiana, Proyección ortogonal es aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección (o a la recta de proyección), estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.

En el plano, la proyección ortogonal es aquella cuyas líneas proyectantes auxiliares son perpendiculares a la recta de proyección L.

Así, dado un segmento AB, bastará proyectar los puntos "extremos" del segmento –mediante líneas proyectantes auxiliares perpendiculares a L–, para determinar la proyección sobre la recta L.

Una aplicación de proyecciones ortogonales son los teoremas de las relaciones métricas en el triángulo mediante las cuales se puede calcular la dimensión de los lados de un triángulo.

El concepto de proyección ortogonal se generaliza a espacios euclidianos de dimensión arbitraria, inclusive de dimensión infinita. Esta generalización juega un papel importante en muchas ramas de matemática y física.

Casos de proyección ortogonal en el plano[editar]

Proyección ortogonal de un punto

• La proyección ortogonal de un punto P en una recta L es otro punto A que se obtiene trazando una línea auxiliar perpendicular a L desde el punto A tal que esta línea pase por P. Lógicamente, si el punto P pertenece a la recta L, coinciden: P = A .

Proyección ortogonal de un segmento

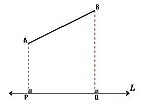
• Caso general: si el segmento dado AB no es paralelo a la recta L, la proyección ortogonal es un segmento PQ que se obtiene trazando líneas perpendiculares a L desde los puntos extremos de AB. La magnitud de la proyección siempre es menor que la del segmento dado.

• Si el segmento PQ y la recta L son paralelos, la proyección será: AB = PQ, que se obtiene de forma análoga.

• Si el segmento AB tiene un punto común con la recta L, la proyección se obtiene de modo similar.

• Si el segmento AB corta a la recta L, la proyección se obtiene de forma análoga.                                   conclusiones.
• - Bastan solo dos puntos, los extremos para hallar la proyección ortogonal de los segmentos sobre la recta R.
• - Aun cuando los segmentos a proyectar tengan distintas longitudes, sus proyecciones ortogonales pueden tener la misma longitud
• RECOMENDACIONES
• El sentido del sentido
• Dos segmentos orientados AB y CD tienen el mismo sentido si sus proyecciones sobre cualquier eje
• coordenado tienen el mismo signo, lo que equivale a decir que son paralelos y la recta que pasa por A y C
• deja a B y D en un mismo semiplano. Mejor sería decir "cualquier recta por A y C " para abarcar el caso
• en que estos puntos coinciden.